Bất đẳng thức Cosi và các dạng bài tập có lời giải chi tiết từ A – Z

Trong bài viết này, chúng tôi sẽ chia sẻ tới các bạn lý thuyết về bất đẳng thức Cosi và các dạng bài tập bất đẳng thức Cosi thường gặp từ cơ bản đến nâng cao trong các đề thi trung học phổ thông và đại học.

Bất đẳng thức cosi

Trong lĩnh vực toán học, bất đẳng thức cosi là khái niệm dùng để chỉ bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Giả sử a₁ ,a₂,…, a_n là các số thực bất kì và b₁, b₂,…, b_n là các số thực dương. Khi đó, ta luôn có:

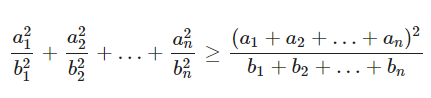
Đẳng thức xảy ra khi và chỉ khi

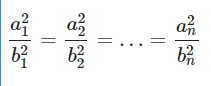
Bất đẳng thức cosi cho 2 số không âm

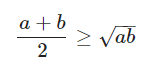
Dấu bằng xảy ra khi và chỉ khi a = b

Bất đẳng thức cosi cho 3 số không âm

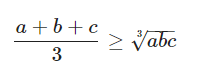
Dấu bằng xảy ra khi và chỉ khi a = b = c

Bất đẳng thức cosi cho 4 số không âm

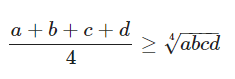
Dấu bằng xảy ra khi và chỉ khi a = b = c = d

Bất đẳng thức cosi cho n số không âm

Với x₁, x₂,…, x_n là n số thực không âm, khi đó ta có

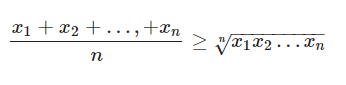
Đẳng thức xảy ra khi và chỉ khi x₁ = x₂ =… = x_n

Dạng tổng quát của bất đẳng thức cosi

Cho x_1,x₂,..,x_n là các số thực dương ta có:

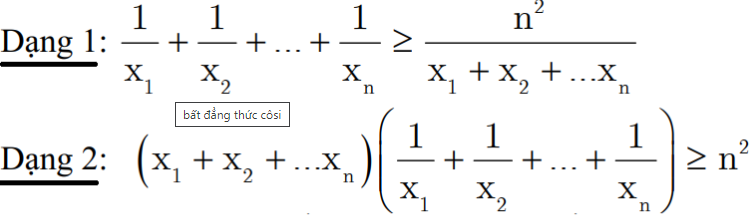
Dấu đẳng thức xảy ra khi và chỉ khi x₁ = x₂ =… = x_n

Cho x_1,x₂,..,x_n là các số thực âm ta có:

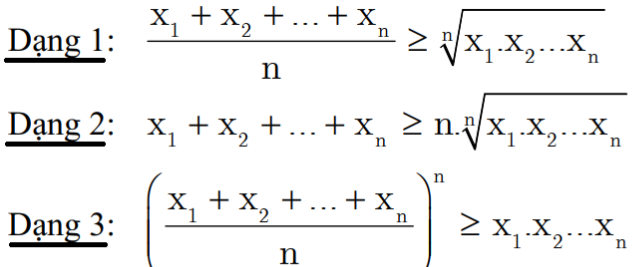
Dấu đẳng thức xảy ra khi và chỉ khi x₁ = x₂ =… = x_n

Các bất đẳng thức cosi đặc biệt

Hệ quả của bất đẳng thức Cosi

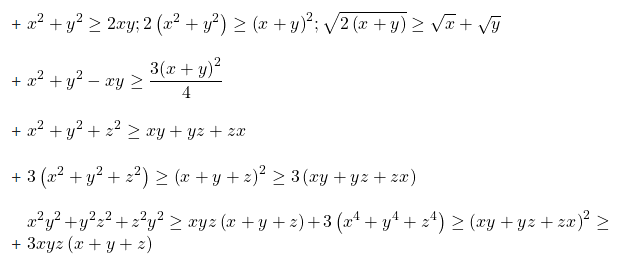
Tham khảo:

• Công thức cấp số cộng
• Công thức cấp số nhân
• Tập xác định của hàm số mũ, lũy thừa, logarit cực đơn giản

Bài tập về bất đẳng thức cosi

Dạng 1: Vận dụng trực tiếp BĐT côsi

Ví dụ1: Cho a, b là số dương thỏa mãn a² + b² = 2. Chứng minh rằng (a+b)⁵ ≥ 16ab √(1+a²)(1+b²)

Lời giải:

Ta có (a+b)⁵ = (a² + 2ab + b² )(a³ + 3ab² + 3a²b + b³)

Áp dụng BĐT cosi ta có:

a² + 2ab + b² ≥ ²√2ab(a² + b²) = 4√ab

(a³ + 3ab² ) (3a²b+b³) ≥ ²√(a³ + 3ab² ) (3a²b+b³) = ⁴√ab (1 + b²)(a² + 1)

=> (a² + 2ab + b² )(a³ + 3ab² + 3a²b + b³) ≥ 16ab√(a² + 1)( b² +1)

=> Do đó (a + b)⁵ ≥ 16ab√(a2 + 1)( b2 +1) điều phải chứng minh

Đẳng thức xảy ra khi và chỉ khi a = b = 1

Ví dụ 2: Cho 2 số không âm a, b. CHứn minh (a + b)(1 + ab) ≥ 4ab

Lời giải

Áp dụng BĐT Cosi cho 2 số thực không âm ta có:

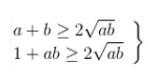
=> (1 + b)(1 + ab) ≥ 2√ab.2√ab = 4ab DPCM

Đẳng thức xảy ra khi và chỉ khi a = b = 1

Dạng 2: Kĩ thuật tách, thêm bớt, ghép cặp

Phương pháp:

• Để chứng minh BĐT ta thường phải biến đổi (nhân chia, thêm, bớt một biểu thức) để tạo biểu thức có thể giản ước được sau khi áp dụng BĐT côsi.
• Khi gặp BĐT có dạng x + y + z ≥ a + b + c (hoặc xyz ≥ abc), ta thường đi chứng minh x + y ≥ 2a (hoặc ab ≤ x2), xây dựng các BĐT tương tự rồi cộng(hoặc nhân) vế với vế ta suy ra điều phải chứng minh.
• Khi tách và áp dụng BĐT côsi ta dựa vào việc đảm bảo dấu bằng xảy ra(thường dấu bằng xảy ra khi các biến bằng nhau hoặc tại biên).

Ví dụ 1: Cho a, b, c là số dương thỏa mãn a + b + c = 3.

Chứng minh rằng 8( a + b )(b + c)(c + a) ≤ (3 + a)(3 + b)(3 + c)

Lời giải

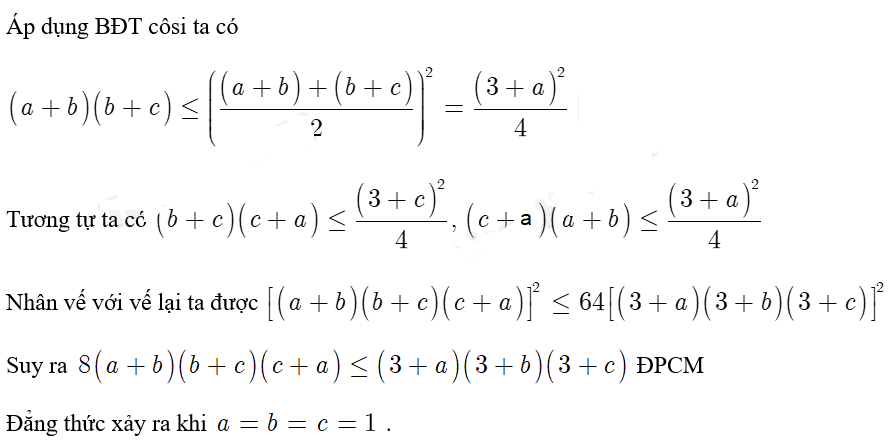
Sau khi đọc xong bài viết của chúng tôi các bạn có thể nắm được lý thuyết về bất đẳng thức cosi và các dạng bài tập bất đẳng thức cosi nhé