Trong bài viết này, chúng tôi sẽ chia sẻ tới bạn đọc về lý thuyết cấp số nhân, tính chất cấp số nhân, công thức tính cấp số nhân và các dạng bài tập về cấp số nhân từ cơ bản đến nâng cao để các bạn cùng tham khảo nhé
Nội dung bài viết
Cấp số nhân là gì?
Cấp số nhân là một dãy số thoả mãn điều kiện kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi. Hằng số này được gọi là công bội của cấp số nhân.
Vì vậy, một cấp số nhân có dạng: a, ar, ar2, ar3, ar4,…trong đó r là công bội và a là số hạng đầu tiên.
Công bội q
q = (Un+ 1)/Un
Trong đó: q là công bội của cấp số nhân.
Tính chất cấp số nhân
uk2=uk–1.uk+1, ∀k≥2
Số hạng tổng quát: un=u1.qn–1, n≥2
Khi q = 0 thì dãy là U1; 0; 0;…; 0;… và Sn = U1 ( Sn : Tổng n số hạng đầu).
Khi q = 1 thì dãy có dạng U1; U1; U1;…;U1;…và Sn = n.U1.
Khi U1 = 0 thì với mọi q, cấp số nhân có dạng 0; 0; 0;…; 0;…và Sn = 0.
Công thức tổng quát cấp số nhân
Nếu (Un) là cấp số nhân với công bội q, ta có công thức truy hồi: un+1=q.un, ∀n≥1,n ∈ N∗ (Với: N* là tập hợp các số tự nhiên lớn hơn 0.)
Ngoài ra, các bạn có thẻ tham khảo: Trung bình cộng là gì? Công thức tính trung bình cộng chuẩn 100%
Tổng n số hạng đầu tiên của một cấp số nhân
Giả sử có cấp số nhân (un) với công bội q. Với mỗi số nguyên dương n gọi sn là tổng n số hạng đầu tiên của nó. Ta có công thức như sau:
sn = u1 + u2 + …+ Un = u1(1 – qn)/(1 – q)
Nếu q = 1 thì cấp số nhân là sn = n.u1
Tổng của cấp số nhân lùi vô hạn
Nếu cấp số nhân có công bội thỏa mãn -1 nhỏ hơn q và q nhỏ hơn 1 thì cấp số nhân được gọi là lùi vô hạn.
Sn = u1(1 – qn)/(1 – q) = u1(qn -1)/(q – 1)
Trong đó: Sn là tổng n số hạng đầu tiên.
Các dạng bài tập về cấp số nhân
Dạng 1: Nhận biết cấp số nhân
Bước 1: Tính q = (Un + 1) / Un ,∀ n ≥ 1
Bước 2: Kết luận:
- Nếu q là số không đổi thì dãy (Un) là cấp số nhân.
- Nếu q thay đổi theo n thì dãy (Un) không là cấp số nhân.
Ví dụ 1: Một cấp số nhân có số hạng thứ nhất là 3 và công bội là 2. Viết 6 số hạng đầu tiên.
Lời giải:
6 số hạng đầu tiên là 3, 6, 12, 24, 48, 96.
Ví dụ 2: Một cấp số nhân có số hạng thứ hai và thứ năm thứ tự là 10, 1250.
a) Tìm số hạng thứ nhất.
b) Viết 6 số hạng đầu tiên.
Lời giải
a) Gọi r là công bội của cấp số nhân. Tỷ số của số thứ năm với số thứ hai là r(5 – 2) = r3 hay r3 = 1250 : 10 = 125 = 53. Từ đó r = 5. Số thứ nhất là 10 : 5 = 2.
b) 2, 10, 50, 250, 1250, 6250.
Dạng 2: Tìm công bội của cấp số nhân
Sử dụng các tính chất của cấp số nhân, biến đổi để tính công bội của cấp số nhân.
Ví dụ: Cho cấp số nhân Un có U1 = 2, U2 = 4. Tính công bội q.
Áp dụng công thức ta có: q = U2 / U1 = 4 / 2 = 2.
Dạng 3: Tìm số hạng của cấp số nhân
Sử dụng công thức tính số hạng tổng quát Un = U1.qn – 1, n ≥ 2.
Ví dụ: Cho cấp số nhân un với u1 = 3, q = -1/2. Tìm u7
Giải:
Áp dụng công thức Un = U1.qn – 1 suy ra u7 = u1.q7-1 = 3 . (-1/2)6 = (3/64)
Dạng 4: Tính tổng cấp số nhân của n số hạng đầu tiên trong dãy
Để tính tổng của cấp số nhân với n số hạng đầu tiên trong dãy số, ta sử dụng công thức:
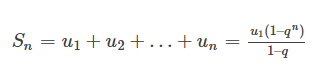
Dạng 5: Tìm cấp số nhân
Tìm các yếu tố xác định một cấp số nhân như: số hạng đầu U1, công bội q.
Tìm công thức cho số hạng tổng quát Un = U1.qn – 1, n ≥ 2.

Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp các bạn nắm được lý thuyết về cấp số nhân là gì từ đó vận dụng giải bài tập nhé

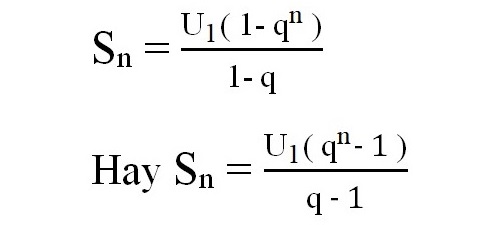
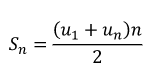

![Định nghĩa và Công thức tính trọng lực chuẩn 100% [Bài tập có lời giải] trong-luc-la-gi](https://kyniemsharp10nam.vn/wp-content/uploads/2021/09/trong-luc-la-gi-150x150.png)