Trong bài trước chúng tôi đã chia sẻ lý thuyết về khoảng cách từ điểm đến mặt phẳng nên hôm nay chúng tôi tiếp tục chia sẻ khoảng cách từ 1 điểm đến 1 đường thẳng có ví dụ minh họa chi tiết trong bài viết dưới đây để các bạn cùng tham khảo nhé
Nội dung bài viết
Khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian là gì?
Trong không gian cho điểm A và đường thẳng Δ bất kỳ. Gọi điểm B là hình chiếu của điểm A lên đường thẳng Δ. Khi đó độ dài đoạn thẳng AB chính là khoảng cách từ điểm A lên đường thẳng Δ.
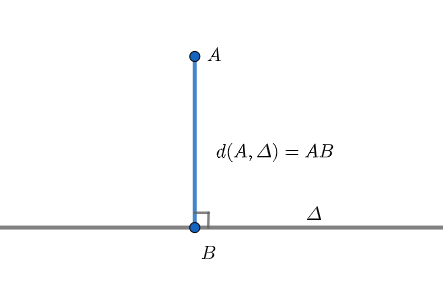
Hay nói cách khác khoảng cách giữa điểm và đường thẳng chính là khoảng cách giữa điểm và hình chiếu của nó trên đường thẳng. Ký hiệu là d(A,Δ).
Tham khảo thêm:
- Viết phương trình đường thẳng đi qua hai điểm
- Tìm m để hàm số đồng biến, nghịch biến trên khoảng chính xác 100%
Cách tính khoảng cách từ một điểm đến một đường thẳng
Phương pháp:
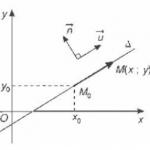
– Cho đường thẳng d: ax + by + c = 0 và điểm M ( x0; y0). Khi đó khoảng cách từ điểm M đến đường thẳng d là![]()
– Cho điểm A( xA; yA) và điểm B( xB; yB) . Khoảng cách hai điểm này là: AB = √(xA – xB)2 + (yB – yA)2
Chú ý: Trong trường hợp đường thẳng d chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng d về dạng tổng quát.
Ví dụ 1:Khoảng cách từ điểm M( 1; -1) đến đường thẳng ( a) : 3x – 4y – 21 = 0 là:
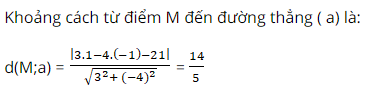
Ví dụ 2: Xét một hệ trục tọa độ Oxyz có đường thẳng Δ: ![]() và 1 điểm có toạn độ A(1; 1; 1). Gọi M là điểm sao cho M ∈ Δ. Tìm giá trị nhỏ nhất của AM?
và 1 điểm có toạn độ A(1; 1; 1). Gọi M là điểm sao cho M ∈ Δ. Tìm giá trị nhỏ nhất của AM?
Lời giải: Khoảng cách AM nhỏ nhất khi AM ⊥ Δ => AMmin=d(A;Δ).

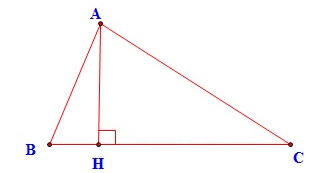
Ví dụ 3: Cho tam giác ABC biết A (1, 2); B (2,3); C(-1,2) Tính độ dài đường cao xuất phát từ đỉnh A xuống cạnh BC
Lời giải:
Độ dài đường cao xuất phát từ đỉnh A đến cạnh BC chính là khoảng cách từ điểm A đến đường thẳng BC. Do đó ta cần viết được phương trình của đường thẳng BC

Ví dụ 4: Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (d): 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) là?
Lời giải:
Do đường thẳng d tiếp xúc với đường tròn ( C) nên khoảng cách từ tâm đường tròn đến đường thẳng d chính là bán kính R của đường tròn
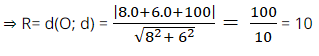
Ví dụ 5: Khoảng cách từ giao điểm của hai đường thẳng (a): x – 3y + 4 = 0 và (b): 2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng là?
Lời giải:
Gọi A là giao điểm của hai đường thẳng ( a) và ( b) tọa độ điểm A là nghiệm hệ phương trình :


![Công thức tính đường chéo hình vuông chính xác 100% [VD có lời giải] cong-thuc-tinh-duong-cheo-hinh-vuong](https://kyniemsharp10nam.vn/wp-content/uploads/2021/09/cong-thuc-tinh-duong-cheo-hinh-vuong-150x150.png)
![Công thức tính độ dài đoạn thẳng chính xác 100% [Bài tập có lời giải] cong-thuc-tinh-do-dai-duong-thang-1](https://kyniemsharp10nam.vn/wp-content/uploads/2021/09/cong-thuc-tinh-do-dai-duong-thang-1-150x150.jpg)