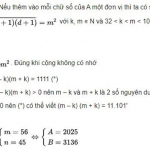Số nguyên tố là kiến thức cơ bản của chương trình học lớp 6 nhưng có rất nhiều bạn học sinh không nắm được số nguyên tố là gì? Tính chất của số nguyên tố cũng như không biết cách tìm số nguyên tố như thế nào? Chính vì vậy trong bài viết dưới đây, Điện máy Sharp Việt Nam sẽ chia sẻ lý thuyết số nguyên tố là gì? Tính chất, cách tìm số nguyên tố và các dạng bài tập từ cơ bản đến nâng cao có lời giải chi tiết để các bạn cùng tham khảo nhé
Nội dung bài viết
Số nguyên tố là gì?
Số nguyên tố là số tự nhiên lớn hơn 1 không phải là tích của hai số tự nhiên nhỏ hơn. Nói cách khác, số nguyên tố là những số chỉ có đúng hai ước số là 1 và chính nó.
Ngược lại, những số có thể chia hết cho 1, chính nó và các số tự nhiên khác nữa được gọi là Hợp số.
Lưu ý: Số 0 và 1 không được coi là số nguyên tố.
Ví dụ: số nguyên tố là 3, 5, 7, 13, 17, 23, 29, 97, 101, 997…
Số nguyên tố nhỏ nhất và có 1 chữ số là số 2
Số nguyên tố nhỏ nhất có 2 chữ số là số 11
Số nguyên tố nhỏ nhất có 3 chữ số là số 101
Số nguyên tố lớn nhất có 2 chữ số là số 97
Số nguyên tố lớn nhất có 3 chữ số là 997
Tính chất của số nguyên tố
Số nguyên tố nhỏ nhất vừa là số nguyên tố chẵn duy nhất là số 2
Không thể giới hạn số lượng số nguyên tố cũng như tập hợp các số nguyên tố. Nói cách khác, số nguyên tố là vô hạn.
Khi hai số nguyên tố nhân với nhau thì tích của chúng không thể là một số chính phương.
Ước tự nhiên nhỏ nhất khác 1 của một số tự nhiên được coi là số nguyên tố.
Ước bé nhất là một số dương khác 1 của một tập hợp số b bất kỳ là một số nguyên tố nếu không vượt quá căn bậc hai của b.
Cách 1: Tìm số nguyên tố bằng cách lặp từng phần tử với bước nhảy 1
Gọi n là số muốn kiểm tra.
Nếu n < 2=””> n không phải là một số nguyên tố.
Nếu n >= 2 thì kiểm tra trong khoảng 2 – (n – 1) có tồn tại số mà n chia hết hay không. Nếu có thì n không phải số nguyên tố, ngược lại thì n là số nguyên tố.
Ví dụ: Muốn kiểm tra số 7.
Ta có: n = 7, trong khoảng (2 – 6) có các số tự nhiên là 3, 4, 5. Ta thấy, 7 không chia hết cho cả 3 số này => 7 là một số nguyên tố.
Cách 2: Tìm số nguyên tố bằng cách lặp từng phần tử với bước nhảy 2
Tương tự như mục trên, nhưng chỉ kiểm tra các số lẻ, sẽ tiết kiệm được nhiều thời gian hơn.
Ví dụ: Muốn kiểm tra số 12.
Ta có: n = 12, trong khoảng (2 – 12) có các số lẽ là 3, 5, 7, 9, 11. Ta thấy, 12 chia hết cho 3 => 12 không phải là một số nguyên tố.
Cách 3: Dùng máy tính cầm tay tìm số nguyên tố
Để kiểm tra xem A có phải số nguyên tố không, bạn thực hiện như sau:
Nhập số nguyên tố, sau đó nhấn dấu “=”.
Nhấn tổ hợp Shift + FACT.
Nếu kết quả hiển thị là A thì A là số nguyên tố.
Nếu kết quả hiển thị là phép nhân thì A không phải số nguyên tố.
Ví dụ, khi kiểm tra số 48 thì sẽ cho ra kết quả là 48 = 24 x 3. => Thừa số nguyên tố của 48 là 2 và 3.
Bài tập về số nguyên tố
Ví dụ 1: Tìm số nguyên tố có ba chữ số, biết rằng nếu viết số đó theo thứ tự ngược lại thì ta được một số là lập phương của một số tự nhiên.
Lời giải
Gọi số tự nhiên đó là a.
Ta có 103 = 1000; 53 = 125 ⇒ 125 ≤ a 3 < 1000 ⇒ 5 ≤ a < 10
Ta có bảng sau:
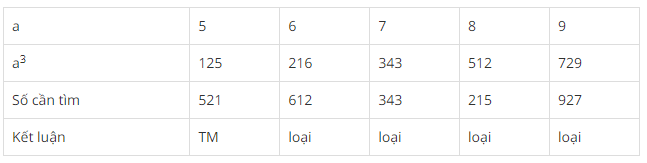
Vậy số cần tìm là 521
Ví dụ 2: Các số sau là số nguyên tố hay hợp số ?
312 ; 213 ; 435 ; 417 ; 3311 ; 67.
Giải
Các số 312, 213, 435 và 417 là hợp số vì chúng lớn hơn 3 và chia hết cho 3.
Số 3311 là hợp số vì số này lớn hơn 11 và chia hết cho 11.
Số 67 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Ví dụ 3: Tổng (hiệu) sau là số nguyên tố hay hợp số ?
a) 3.4.5 + 6.7 ; b) 7.9.11.13 – 2 3.4.7;
c) 5.7 + 11.13.17 ; d) 16354 + 67541.
Giải
a) Mỗi số hạng của tổng đều chia hết cho 3. Tổng chia hết cho 3 và lớn hơn 3 nên là hợp số.
b) Mỗi số hạng của hiệu đều chia hết cho 7. Hiệu chia hết cho 7 và lớn hơn 7 nên là hợp số.
c) Mỗi số hạng của tổng đều là số lẻ nên tổng là số chẵn. Tổng chia hết cho 2 và lớn hơn 2
nên là hợp số.
d) Tổng tận cùng bằng 5 nên chia hết cho 5. Tổng này lại lớn hơn 5 nên là hợp số.
Ví dụ 4: Chứng minh rằng nếu ba số a, a+k, a+2k đều là các số nguyên tố lớn hơn 3, thì k chia hết cho 6
Lời giải:
Do a, a + k, a + 2k đều là nguyên tố lớn hơn 3 nên đều là số lẻ và không chia hết cho 3.
Vì a và a + k cùng lẻ nên a + k – a = k ⋮ 2. (1)
Vì a, a + k, a + 2k đều không chia hết cho 3 nên khi chia cho 3 ít nhất hai số có cùng số dư, khi đó:
Nếu a và a + k có cùng số dư, thì suy ra: (a+k) – a = k ⋮ 3
Nếu a + k và a + 2k có cùng số dư, thì suy ra: (a+2k )- (a+k)= k ⋮ 3
Nếu a và a + 2k có cùng số dư, thì suy ra: ( a + 2k ) – a = 2k 3 nhưng (2,3) = 1 nên k 3
Vậy, ta luôn có k chia hết cho 3 (2)
Từ (1),(2) và do (2,3)=1 ta suy ra k ⋮ 6, đpcm.
Nhận xét: Trong lời giải trên, ta đã định hướng được rằng để chứng minh k ⋮ 6 thì cần chứng minh k ⋮ 2 và k ⋮ 3 và ở đó:
Việc chứng minh k ⋮ 2 được đánh giá thông qua nhận định a, a + k,a + 2k đều là nguyên tố lẻ hơn kém nhau k đơn vị.
Việc chứng minh k ⋮ 3 được đánh giá thông qua nhận định ba số lẻ không chia hết cho 3 thì có ít nhất hai số có cùng số dư và như vậy hiệu của hai số đó sẽ chia hết cho 3.
Ví dụ 5: Tìm số nguyên tố, biết rằng số đó bằng tổng của hai chữ số nguyên tố và bằng hiệu của hai số nguyên tố
Lời giải
Giả sử a, b, c, d, e là các số nguyên tố (d > e)
Theo bài ra ta có: a = b + c = d – e (*)
Từ (*) ⇒ a > 2 ⇒ a là số nguyên tố lẻ
+ b + c = d – e là số lẻ.do b, d là các số nguyên tố ⇒ b, d là số lẻ ⇒ c, e là số chẵn.
+ c = e = 2 (do e, c là các số nguyên tố)
+ a = b + 2 = d – 2 ⇒ d = b + 4,vậy ta cần tìm số nguyên tố b sao cho b + 2, b + 4 cũng là số nguyên tố
+ b = 3
Vậy số nguyên tố cần tìm là 5
Hy vọng với những kiến thức về số nguyên tố là gì và cách tìm số nguyên tố có thể giúp các bạn hệ thống lại kiến thức từ đó áp dụng vào làm bài tập đơn giản và chính xác nhé
