Trong bài viết dưới đây chúng tôi sẽ chia sẻ phương pháp tìm m để hàm số đồng biến trên khoảng, nghịch biến trên khoảng với nhiều cách khác nhau như cô lập tham số, nhẩm nghiệm, nghiệm và dấu của tam thức bậc 2,..giúp bạn có thể áp dụng vào làm bài tập nhanh chóng nhé
Nội dung bài viết
Phương pháp tìm m để hàm số đồng biến, nghịch biến trên khoảng
Cho hàm số f(x,m) xác định và có đạo hàm trên khoảng (a;b). Tìm giá trị của m để hàm số f(x,m) đơn điệu trên khoảng (a;b).
1. Tìm m để hàm số đơn điệu trên khoảng
Cho hàm số y = f( x) có đạo hàm trên khoảng (a, b):
- Hàm số y = f( x) đồng biến trên khoảng (a, b) khi và chỉ khi f'( x) ≥ 0 với mọi giá trị x thuộc khoảng (a, b). Dấu = chỉ được xảy ra tại hữu hạn điểm..
- Hàm số y = f( x) nghịch biến trên khoảng (a, b) khi và chỉ khi f'( x) ≤ 0 với mọi giá trị x thuộc khoảng (a, b). Dấu = chỉ được xảy ra tại hữu hạn điểm
Như vậy muốn hàm số f(x) có đạo hàm trên khoảng (a;b) thì f(x) cần phải xác định và liên tục trên khoảng (a;b).
Do đó để giải quyết bài toán tìm m để hàm số đồng biến trên khoảng cho trước hay tìm m để hàm số nghịch biến trên khoảng cho trước thì ta nên thực hiện theo thứ tự như sau:

2. Đánh giá đạo hàm khi có tham số
Đến bước này các bạn cần đưa ra sự lựa chọn phương pháp đánh giá đạo hàm. Theo thứ tự các bạn nên ưu tiên như sau:
Cách 1:

Cách 2: Cô lập tham số m
Cô lập được tham số m từ bất phương trình f'(x,m) ≥ 0 với mọi x thuộc khoảng (a;b) chẳng hạn.
Ta sẽ thu được bất phương trình dạng m ≥ g(x) với mọi x thuộc khoảng (a;b). Hoặc m ≤ g(x) với mọi x thuộc khoảng (a;b). Khi đó, hãy chú ý rằng nếu g(x) có giá trị lớn nhất hay nhỏ nhất thì:
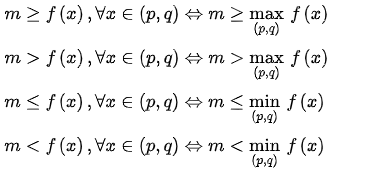
Còn trong trường hợp không có giá trị lớn nhất hay nhỏ nhất thì ta có thể xét đến cận trên đúng hoặc cận dưới đúng của g(x). Và lúc này dấu = cần xem xét cẩn thận.
Cách 3: Nghiệm và dấu của tam thức bậc 2:
Hai cách trên không sử dụng được nữa thì ta phải áp dụng các kiến thức về nghiệm và dấu của tam thức bậc 2 vào giải quyết.
Tham khao thêm:
- 7 hằng đẳng thức đáng nhớ
- Các dạng viết phương trình tiếp tuyến của đồ thị hàm số từ A – Z
- Cách xét tính chẵn lẻ của hàm số chính xác 100%
Bài tập tìm m để hàm số đồng biến, nghịch biến trên khoảng
Dạng 1: Tùy theo tham số m khảo sát tính đơn điệu của hàm số
Trong chương trình, đây là dạng toán thường gặp đối với hàm số đa thức bậc 3. Nếu là hàm đa thức bậc 3 thì chúng ta có thể áp dụng kiến thức sau:

Ví dụ 1: Tùy theo m khảo sát tính đơn điệu của hàm số
y = 1/3x3 – ½m(m + 1)x2 + m3x + m2 + 1
Lời giải:
Hàm số đã cho xác định trên R

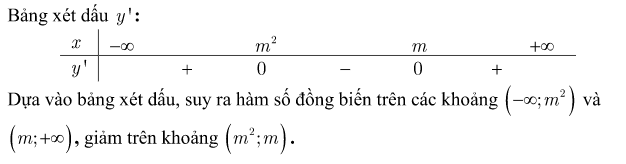
Dạng 2: Tìm m để hàm số đồng biến, nghịch biến trên R
Phương pháp giải: sử dụng định lý về điều kiện cần
- Nếu hàm số f đồng biến trên R thì f ‘(x) ≥ 0 với mọi x ∈ R
- Nếu hàm số f nghịch biến trên R thì f ‘(x) ≤ 0 với mọi x ∈ R




Dạng 3 : Tìm m để hàm số đơn điệu trên tập con của R.


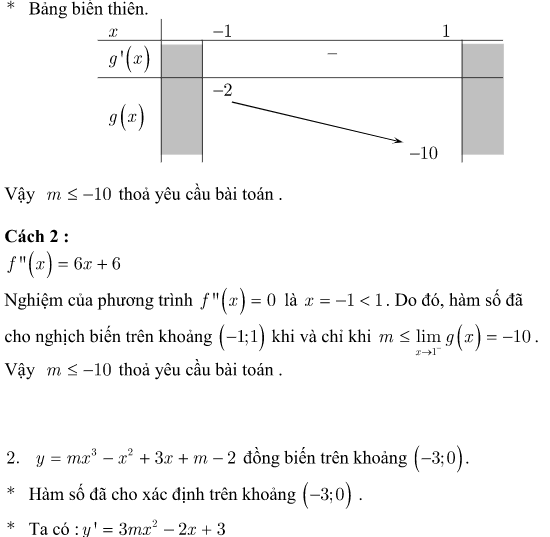


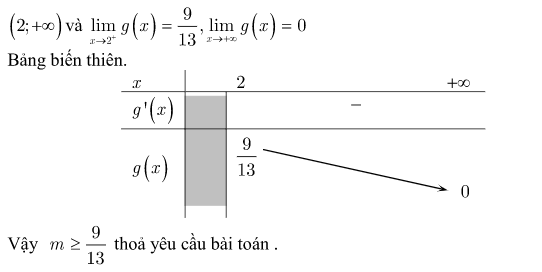
Dạng 4. Biện luận đơn điệu của hàm phân thức
Phương pháp giải được chia thành 2 loại như sau:
Loại 1. Tìm điều kiện của tham số để hàm y = ax + b/cx + d đơn điệu trên từng khoảng xác định.
Tính y’ = (ad – cb)/ (cx + d)2
- Hàm số đồng biến trên từng khoảng xác định của nó ⇔ y’ > 0 ⇔ ad –cb > 0
- Hàm số nghịch biến trên từng khoảng xác định của nó ⇔ y’ < 0 ⇔ ad –cb < 0

Ví dụ : Ví dụ 2. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = (x + 6)/ (x + 5m) nghịch biến trên khoảng (10; +∞)?
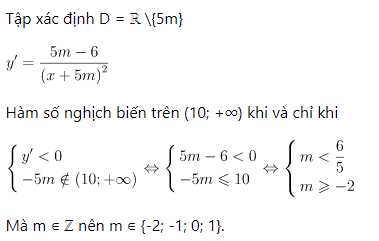
Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp biết cách tìm m để hàm số đồng biến trên khoảng chính xác nhé

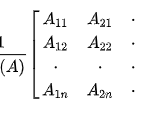
![Động năng là gì? Công thức tính động năng chính xác 100% [VD] cong-thuc-tinh-dong-nang-1](https://kyniemsharp10nam.vn/wp-content/uploads/2021/10/cong-thuc-tinh-dong-nang-1-150x67.png)

![Số nguyên tố là gì? Cách tìm số nguyên tố chính xác 100% [Bài tập] so-nguyen-to-la-gi](https://kyniemsharp10nam.vn/wp-content/uploads/2021/10/so-nguyen-to-la-gi-150x150.png)