Trong bài viết dưới đây, chúng tôi sẽ chia sẻ tới các bạn kiến thức về lăng trụ tam giác đều bao gồm: định nghĩa, tính chất, diện tích xung quanh, diện tích toàn phần và thể tích giúp các bạn củng cổ lại kiến thức để vận dụng giải các bài tập
Nội dung bài viết
Lăng trụ tam giác đều là gì?
Lăng trụ tam giác đều là hình lăng trụ có hai đáy là hai tam giác đều bằng nhau.
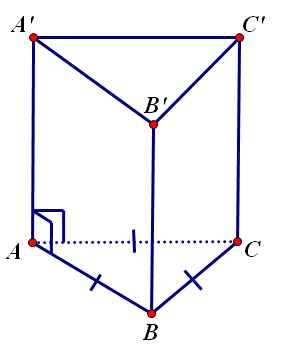
Tính chất
- Hai đáy là hai tam giác đều bằng nhau do đó các cạnh đáy bằng nhau.
- Các mặt bên là các hình chữ nhật bằng nhau.
- Các mặt bên và hai đáy vuông góc với nhau.
Công thức tính diện tích xung quanh lăng trụ tam giác đều
Diện tích xung quanh lăng trụ tam giác đều bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao.
Sxq = P.h
Trong đó:
- p: chu vi đáy.
- h: chiều cao
Công thức tính diện tích toàn phần lăng trụ tam giác đều
Diện tích toàn phần của lăng trụ tam giác đều bằng tổng diện tích các mặt bên và diện tích 2 đáy
Stp = Sxq + 2S = 3.a.h + a2 . (√3)/4.
Trong đó:
- a là chiều dài cạnh đáy
- h là chiều cao
Công thức tính thể tích lăng trụ tam giác đều
Thể tích lăng trụ tam giác đều bằng diện tích khối lăng trụ nhân với chiều cao hoặc bằng căn bậc 2 của ba nhân với lập phương tất cả các cạnh bên, sau đó tất cả chia cho 4.
V = S.h = (√3)/4a3h
Trong đó
- a là chiều dài cạnh đáy
- h là chiều cao
Tham khảo:
Các dạng bài tập về lăng trụ tam giác đều
Ví dụ 1: Tính thể tích khối trụ Δ đều ABCA’B’C’ có độ dài cạnh đáy bằng 8cm và mặt phẳng A’B’C’ tạo với mặt đáy ABC một góc bằng 60 độ.
Gọi I là trung điểm của đoạn thẳng BC ta có:
AI vuông góc BC (theo tính chất đường trung tuyến của một tam giác đều)
A’I vuông góc BC (Vì A’BC là tam giác cân)
Góc A’BC, ABC = góc AIA’ = 600
![]()
Diện tích tam giác ABC:
S = a2 . (√3)/4 = 82x (√3)/4 = 2√3 cm2
Thể tích khối lăng trụ tam giác đứng ABCA’B’C’ là:
V = S.h = 12 x 2√3 = 24√3 cm3
Ví dụ 2: Cho hình lăng trụ tam giác đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích toàn phần của hình lăng trụ đứng là?
Lời giải
– Diện tích xung quanh hình lăng trụ đứng ABCD.A’B’C’D’ = p x h = (2(AB + BC)) x 2,5 = 45 (cm2).
– Diện tích đáy hình chữ nhật ABCD = 4 x 5 = 20 (cm2).
– Diện tích toàn phần hình lăng trụ đứng ABCD.A’B’C’D’ = Sxq + 2.S = 45 + 2 x 20 = 85 (cm2).
Ví dụ 3: Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 3cm BC = 6cm, chiều cao h = 3,5cm. Diện tích xung quanh của hình ABCD.A’B’C’D’?
Giải
– Chu vi đáy hình chữ nhật ABCD= 2(AB + BC)= 2(3 + 6) = 18 (cm).
– Diện tích xung quanh hình lăng trụ đứng ABCD.A’B’C’D’ = p.h = 18.3,5= 63 (cm2).
Ví dụ 4: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a√3, góc giữa và đáy là 60º. Gọi M là trung điểm của . Tìm thể tích của khối chóp M.A’B’C’
Lời giải:
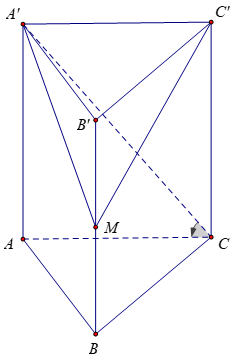
Do AA’ vuông góc với tam giác ABC nên suy ra
(A’C,(ABC)) = góc A’CA = 60º
Ta có AA’ = AC . Tan A’CA = a√3.tan60º = 3a
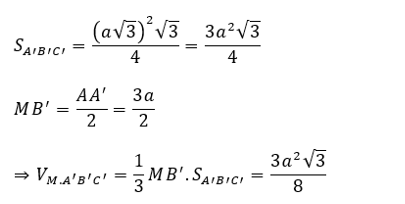
Hy vọng với những thông tin mà chúng tôi vừa chia sẻ có thể giúp bạn nắm vững được kiến thức lăng trụ tam giác đều trong suốt quá trình học tập.


![Diện tích xung quanh hình trụ, diện tích toàn phần hình trụ chuẩn 100% [Có ví dụ minh họa]] dien-tich-xung-quanh-hinh-tru](https://kyniemsharp10nam.vn/wp-content/uploads/2021/05/dien-tich-xung-quanh-hinh-tru-150x150.jpg)