Trong bài viết dưới đây, chúng tôi sẽ chia sẻ tới bạn đọc diện tích xung quanh hình nón và diện tích toàn phần hình nón để các bạn có thể vận dụng làm các bài tập. Các bạn cùng tham khảo nhé
Nội dung bài viết
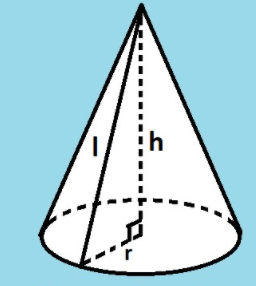
Công thức tính diện tích xung quanh hình nón
Diện tích xung quang khối nón bằng tích của bán kính đáy hình nón, đường sinh hình nón và hằng số pi
Sxq = πrl
Trong đó:
Sxq: là diện tích xung quanh
π: là hằng số Pi = 3,14
r: Bán kính vòng tròn đấy hình nón
l: đường sinh của hình nón
Công thức tính diện tích toàn phần khối nón
Diện tích toàn phần khối nón bằng diện tích xung quang hình nón cộng với diện tích mặt đáy hình nón.
Ví dụ 1: Cho hình nón có bán kính đáy R = 3, chiều cao h = 4. Tìm Sxq hình thoi
Lời giải:
Độ dài đường sinh l = √R2 + h2=√32+42 = 5
Vậy diện tích xung quanh là
Sxq = πRl= 3.5.π = 15π cm2
Ví dụ 2: Cho một hình nón bất kỳ có đáy là tâm O và đỉnh A. Bán kính r nối từ tâm đáy hình nón tới một cạnh đáy bất kỳ của hình nón dài 6 cm, chiều dài đường sinh nối từ đỉnh A xuống một điểm bất kỳ trên đáy dài 8 cm. Hỏi Sxq hình nón bằng bao nhiêu?
Áp dụng công thức : Sxq = π.r.l = π x 8 x 6 = 48π (cm)².
Ví dụ 3: Cho một hình nón bất kỳ có đáy là tâm O và đỉnh A. Bán kính r nối từ tâm đáy hình nón tới một cạnh đáy bất kỳ của hình nón dài 5cm. Hỏi diện tích toàn phần của hình nón bằng bao nhiêu, biết chiều dài đường sinh nối từ đỉnh A xuống một điểm bất kỳ trên đáy dài 7cm.
Hướng dẫn giải:
Áp dụng công thức: Stp = π.r.l + π.r² = π x 5 x 7 + π x 5² = 60π (cm)².
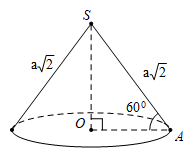
Ví dụ 4: Cho hình nón tròn xoay có đỉnh là S; O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 600.Tính Sxq của hình nón
Lời giải
Gọi A là một điểm thuộc đường tròn đáy hình nón.
Theo giải thiết ta có đường sinh SA = a√2 và góc giữa đường sinh và mặt phẳng đáy là
góc SAO = 600 .
Trong tam giác vuôn SAO, ta có:
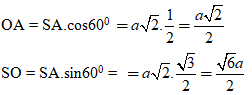
Diện tích xung quanh hình nón là:
Sxq = πRl = π.a√2/2.a√2 = πR2
Ví dụ 5: Cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng 3a2. Diện tích xung quanh của (N) là:
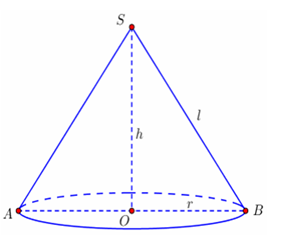
Do cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón nên thiết diện qua trục là mặt phẳng (SAB) – với AB là đường kính của đường tròn đáy.
Theo giả thiết tam giác SAB là tam giác vuông cân tại S và có diện tích 3a2 nên
SABC = Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón cực hay SA2 = 3a2 ⇒ SA = √6a
Khi đó, độ dài đường sinh của hình nón là
l = SA = √6a
Do tam giác SAB là tam giác vuông cân tại S nên
AB = SA.√2 = √6a.√2 = 2√3a
Suy ra, đường cao của hình nón là:
h = SO = AB/2 = √3a
Bán kính đường tròn đáy là R = AB/2 = a√3 .
Diện tích xung quanh của (N) là:
Sxq = π.R.l = π.a√3.a.√6 = 3√2πa2
Bên trên chính là toàn bộ công thức tính diện tích xung quanh và diện tích toàn phần hình nón mà chúng tôi vừa chia sẻ có thể giúp bạn áp dụng giải nhanh các bài tập nhé
