Cách xét tính chẵn lẻ của hàm số chính xác 100% [ Bài tập minh họa]

Bạn tốn khá nhiều thời gian nhưng vẫn không xác định được hàm số trong bài tập về nhà là hàm số chẵn hay hàm số lẻ. Chính vì vậy, chúng tôi sẽ hướng dẫn các bạn cách xét tính chẵn lẻ của hàm số chi tiết trong bài viết dưới đây để các bạn cùng tham khảo nhé

Hàm số chẵn lẻ là gì?

Cho hàm số y = f(x) có tập xác định D.

• Hàm số f được gọi là hàm số chẵn nếu với ∀x ∈ D thì −x ∈ D và f(x) =f(−x).

• Hàm số f được gọi là hàm số lẻ nếu với ∀x ∈ D thì −x ∈ D và f(x) = −f(−x)

Lưu ý:

• Điều kiện thứ nhất gọi là điều kiện tập xác định đối xứng qua số 0.
• Một hàm số không nhât thiết phải là hàm số chẵn hoặc hàm số lẻ.

Ví dụ 1: D = (-2;2) là tập đối xứng qua số 0, còn tập D’=[-2;3] là không đối xứng qua 0. Tập R=(−∞;+∞) là tập đối xứng.

Ví dụ 2: Hàm số y = 2x + 1 không là hàm số chẵn, cũng không là hàm số lẻ vì:

Tại x = 1 có f(1) = 2.1 + 1 = 3

Tại x = -1 có f(-1) = 2.(-1) + 1 = -1

⇒ Hai giá trị f(1) và f(-1) không bằng nhau và cũng không đối nhau

Đồ thị của hàm số chẵn lẻ

Hàm số chẵn có đồ thị nhận trục tung Oy làm trục đối xứng.

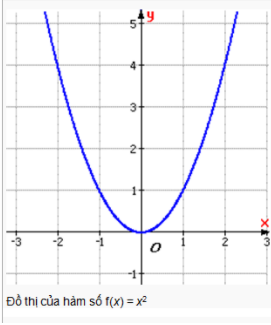
Hàm số lẻ có đồ thị nhận gốc toạ độ O làm tâm đối xứng.

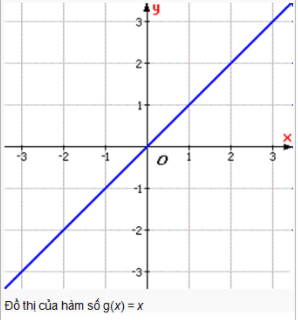
Cách xét tính chẵn lẻ của hàm số, hàm số có trị tuyệt đối

Để xét tính chẵn lẻ của hàm số các bạn cần sử dụng định nghĩa và quy trình xét hàm số chẵn, lẻ cụ thể như sau:

Sử dụng định nghĩa

Hàm số y = f(x) xác định trên D

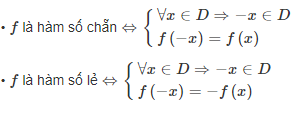
Lưu ý:

• Một hàm số có thể không chẵn cũng không lẻ
• Đồ thị hàm số chẵn nhận trục Oy làm trục đối xứng
• Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng

Các bước xét tính chẵn, lẻ của hàm số

Bước 1. Tìm tập xác định D của hàm số.

Bước 2. Kiểm tra:

• Nếu ∀x ∈ D ⇒−x ∈ D thì chuyển qua bước 3.
• Nếu tồn tại x₀ ∈ D mà −x₀ ∉ Dthì kết luận hàm không chẵn cũng không lẻ.

Bước 3. Xác định f(−x)và so sánh với f(x):

• Nếu f(−x) = f(x) thì kết luận hàm số là chẵn.
• Nếu f(−x) = −f(x) thì kết luận hàm số là lẻ.
• Nếu tồn tại một giá trị ∃ x₀ ∈ D mà f(-x0 ) ≠ ± f(x0) kết luận hàm số không chẵn cũng không lẻ.

Tham khảo thêm:

• Giải hệ phương trình bằng phương pháp cộng đại số chuẩn 100%
• Công thức tổ hợp, chỉnh hợp, hoán vị và các dạng bài tập chi tiết từ A – Z
• Công thức cấp số cộng

Bài tập xét tính chẵn lẻ của hàm số

Ví dụ 1: Xét tính chẵn lẻ của các hàm số sau:

a) y = |x|;

b) y = (x + 2)²;

c) y = x³ + x;

d) y = x² + x + 1.

Lời giải

a) Đặt y = f(x) = |x|.

TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

f(–x) = |–x| = |x| = f(x).

Vậy hàm số y = |x| là hàm số chẵn.

b) Đặt y = f(x) = (x + 2)².

TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

f(–x) = (–x + 2)² = (x – 2)² ≠ (x + 2)² = f(x)

f(–x) = (–x + 2)² = (x – 2)² ≠ – (x + 2)² = –f(x).

Vậy hàm số y = (x + 2)² làm hàm số không chẵn, không lẻ.

c) Đặt y = f(x) = x³ + x.

TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

f(–x) = (–x)³ + (–x) = –x³ – x = – (x³ + x) = –f(x)

Vậy y = x³ + x là hàm số lẻ.

d) Đặt y = f(x) = x² + x + 1.

TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ x² + x + 1 = f(x)

f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ –(x² + x + 1) = –f(x)

Vậy hàm số y = x² + x + 1 là hàm số không chẵn, không lẻ.

Ví dụ 2: Xét tính chẵn lẻ của hàm số : y = f(x) = √2x + 8 – 5

TXĐ : 2x + 8 ≥ 0 <=> x ≥ – 4

D = [-4; + ∞)

ta có : 5 ∈ D mà – 5 ∉ D => D không là tập đối xứng.

vậy : hàm số không chẵn, không lẻ.

Ví dụ 3: Tìm m để hàm số sau là hàm số chẵn.

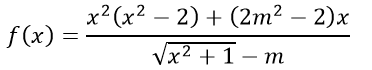
Lời giải

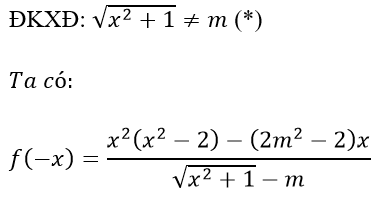
Giả sử hàm số chẵn suy ra f(-x) = f(x) với mọi x thỏa mãn điều kiện (*)

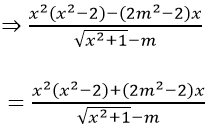
với mọi x thỏa mãn (*)

⇒ 2(2m² – 2)x = 0 với mọi x thỏa mãn (*)

⇔ 2m² – 2 = 0 ⇔ m = ± 1

Với m = 1 ta có hàm số là

ĐKXĐ : √(x2+1) ≠ 1 ⇔ x ≠ 0

Suy ra TXĐ: D = R\{0}

Dễ thấy với mọi x ∈ R\{0} thì -x ∈ R\{0} và f(-x) = f(x)

Do đó là hàm số chẵn.

TXĐ: D = R

Dễ thấy với mọi x ∈ R thì -x ∈ R và f(-x) = f(x)

Do đó là hàm số chẵn.

Vậy m = ± 1 là giá trị cần tìm.

Ví dụ 3: Xét tính chẵn, lẻ của các hàm số sau:
a. y = f(x) =√1 – x + √1+x

b. y = f(x) = ³√2x−3 – ³√2x+3

Lời giải

a. Tập xác định D = [-1; 1] là tập đối xứng.

Xét: f(–x) = √1 – (-x) + √1+(-x) = =√1 – x + √1+x = f(x)

Vậy, hàm số chẵn.

b. Hàm số xác định trên D = R là tập đối xứng. Ta có:

f(-x) = ³√2(-x)−3 – ³√2(-x)+3 = ³√2x−3 – ³√2x+3 = f(x)

Vậy, hàm số là chẵn.

Sau khi đọc xong bài viết của chúng tôi các bạn có thể biết cách xét tính chẵn lẻ của hàm số để áp dụng vào làm các bài tập từ cơ bản đến nâng cao nhanh chóng và chính xác nhất