Giá trị tuyệt đối là những kiến thức các bạn học sinh đã được tiếp cận từ bậc trung học cơ sở. Bài viết dưới đây sẽ giải thích chi tiết về giá trị tuyệt đối là gì, dấu giá trị tuyệt đối, tính chất giá trị tuyệt đối, phương trình chứa dấu giá trị tuyệt đối, bất phương trình chứa dấu giá trị tuyệt đối đi kèm các dạng bài tập phổ biến có lời giải chi tiết. Bạn cùng theo dõi nhé
Giá trị tuyệt đối là kiến thức cơ bản được học từ trung học cơ sở nhưng có rất nhiều các bạn học sinh không nắm vững được và các phương pháp giải giá trị tuyệt đối như thế nào? Sau đây, chúng tôi sẽ chia sẻ lý thuyết giá trị tuyệt đối là gì và các dạng bài tập liên quan nhé
Nội dung bài viết
Giá trị tuyệt đối là gì?
Giá trị tuyệt đối của số hữu tỉ x, kí hiệu là|x|,là khoảng cách từ điểm x tới điểm 0 trên trục số.
- Nếu x > 0 thì |x| = x.
- Nếu x = 0 thì |x| = 0.
- Nếu x < 0 thì |x| = -x.
Có thể hiểu đơn giản giá trị tuyệt đối của một số là giá trị không âm của số đó, tức là nếu số đó lớn hơn hoặc bằng 0, thì giá trị tuyệt đối của nó không thay đổi, và nếu số đó là âm, thì giá trị tuyệt đối sẽ là số dương tương ứng.
Từ định nghĩa trên ta có thể viết như sau:
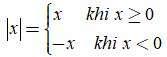
Ví dụ:
Nếu 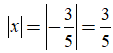
Nếu x = 8 thì |x| = |8| = 8.
Nếu x = 0 thì |x| = 0
Nếu x = -2 thì |x| = 2
Chú ý: Với mọi x ∈ Q ta luôn có |x| ≥ 0, |x| = |-x|, |x| > x.
Tính chất của giá trị tuyệt đối
Giá trị tuyệt đối của số không âm là chính nó, giá trị tuyệt đối của số âm là số đối của nó.
- Nếu a ≥ 0 => |a| = a
- Nếu a < 0 => |a| = -a
- Nếu x – a ≥ 0 => |x – a| = x – a
- Nếu x – a ≤ 0 => |x – a| = a – x
Giá trị tuyệt đối của mọi số đều không âm |a| ≥ 0 với mọi a ∈ R. Cụ thể:
- |a| =0 <=> a = 0
- |a| ≠0 <=> a ≠0
Hai số bằng nhau hoặc đối nhau thì có giá trị tuyệt đối bằng nhau và ngược lại hai số có giá trị tuyệt đối bằng nhau thì chúng là hai số bằng nhau hoặc đối nhau.
- |a| = |b| ↔ a = b hoặc a = -b
Mọi số đều lớn hơn hoặc bằng đối của giá trị tuyệt đối của nó và đồng thời nhỏ hơn hoặc bằng giá trị tuyệt đối của nó.
- -|a| ≤ a ≤ |a| và -|a| = a ↔ a ≤ 0; a = |a| ↔ a ≥ 0
Trong hai số âm số nào nhỏ hơn thì có giá trị tuyệt đối lớn hơn. Nếu a < b < 0 → |a| > |b|
Trong hai số dương số nào nhỏ hơn thì có giá trị tuyệt đối nhỏ hơn. Nếu 0 < a < b → |a| < |b|
Giá trị tuyệt đối của một tích bằng tích các giá trị tuyệt đối: |a.b| = |a|.|b|
Giá trị tuyệt đối của một thương bằng thương hai giá trị tuyệt đối.
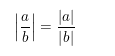
Bình phương của giá trị tuyệt đối của một số bằng bình phương số đó.
- |a|2 = a2
Tổng hai giá trị tuyệt đối của hai số luôn lớn hơn hoặc bằng giá trị tuyệt đối của hai số, dấu bằng xảy ra khi và chỉ khi hai số cùng dấu.
- |a| + |b| ≥ |a + b| và |a| + |b| = |a + b| ↔ ab ≥ 0
Tham khảo:
Phương trình chứa dấu giá trị tuyệt đối
Phương trình chứa dấu giá trị tuyệt đối là phương trình có chứa ẩn trong dấu giá trị tuyệt đối.
Phương trình có dạng: |f(x)| = a; (a>0)
Cách giải : |f(x)| = a;(a>0)⇔ f(x) = a hoặc f(x) = −a
Ví dụ: Giải phương trình |x + 1| = 2
Lời giải:

Phương trình có dạng : |f(x)| = |g(x)|
Cách giải : |f(x)| = |g(x)| ⇔ f(x) = g(x) hoặc f(x) = −g(x)
Ví dụ: Giải phương trình |x – 3| = |2 + 2x|

Bất phương trình chứa dấu giá trị tuyệt đối
Là bất phương trình có chứa ẩn trong dấu giá trị tuyệt đối. Thông thường, ta gặp ba dạng và sau đây là cách giải :
- |f(x)| > g(x) ⇔ f(x) > g(x) hoặc f(x) < −g(x)
- |f(x)| < |g(x)| ⇔ [f(x)]2 < [g(x)]2
- |f(x)| < g(x) ⇔ −g(x) < f(x) < g(x)
Các dạng bài toán liên quan đến giá trị tuyệt đối
Trong chương trình trung học và trung học phổ thông, thường có 4 dạng toán phổ biến liên quan đến dấu giá trị tuyệt đối.
Dạng 1: |A(x)| = k (Trong đó A(x) là biểu thức chứa x, k là một số cho trước)
Cách giải:
– Nếu k < 0 thì không có giá trị nào của x thoả mãn đẳng thức ( Vì giá trị tuyệt đối của mọi số đều không âm )
– Nếu k = 0 thì ta có |A(x)| = 0 → A(x) = 0
– Nếu k > 0 thì ta có: |A(x)| = k → A(x) = k hoặc A(x) = -k
Ví dụ: Giải phương trình sau:
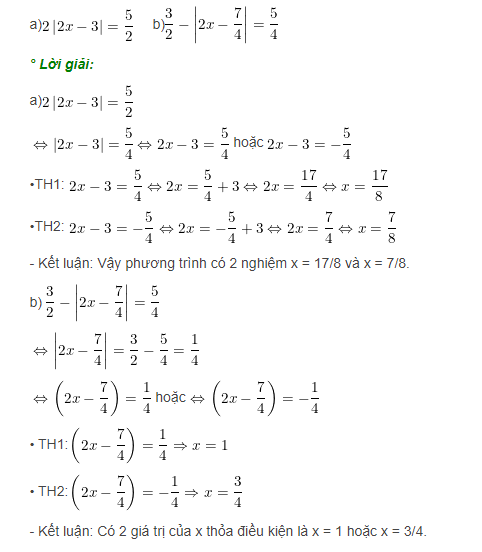
Dạng 2: Phương trình chứa dấu giá trị tuyệt đối dạng |P(x)| = |Q(x)|
Với dạng toán giải phương trình chứa dấu giá trị tuyệt đối xuất hiện với một biến số và đòi hỏi bạn cần giải phương trình này thành nhiều trường hợp.

Dạng 3: Rút gọn biểu thức và tính giá trị biểu thức
Phương pháp giải:
Với |a(x) + b + c| = d
Ta sẽ tính các giá trị bên trong giá trị tuyệt đối


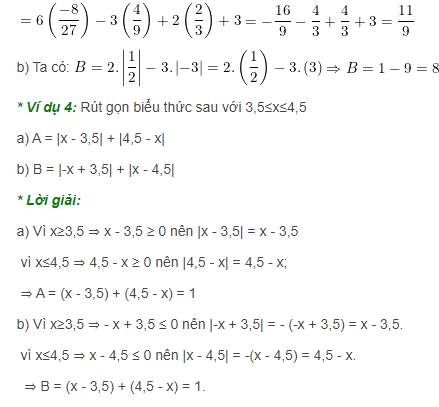
Dạng 4: Đẳng thức chứa nhiều dấu giá trị tuyệt đối
Phương pháp giải:
Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối: |a(x)| + |b(x)| + |c(x)| = m
Căn cứ bảng trên xét từng khoảng giải bài toán (đối với từng điều kiện tương ứng)
Ví dụ Giải bất phương trình sau đây |2 – 5x| >= x + 1.


Ứng dụng của giá trị tuyệt đối trong khoa học và đời sống
Giá trị tuyệt đối có nhiều ứng dụng quan trọng trong nhiều lĩnh vực, từ toán học đến khoa học, kỹ thuật, và cuộc sống hàng ngày. Dưới đây là một số ứng dụng phổ biến của giá trị tuyệt đối:
- Khoảng cách và Tính toán Vị trí: Giá trị tuyệt đối được sử dụng để tính khoảng cách giữa hai điểm trên trục số. Ví dụ, nếu bạn có hai điểm A và B trên trục số, khoảng cách giữa chúng có thể được tính bằng |B – A|.
- Quy tắc Tìm Giá trị Lớn Nhất và Nhỏ Nhất: Trong toán học, giá trị tuyệt đối được sử dụng để tìm giá trị lớn nhất và nhỏ nhất của một hàm số trong một khoảng cụ thể. Điều này thường xuất hiện trong các bài toán tối ưu hóa.
- Đo Kích thước và Tính Toán Tích phân: Giá trị tuyệt đối thường được sử dụng trong tích phân để đảm bảo giá trị không âm của các đại lượng. Nó cũng được sử dụng để đo kích thước vật lý và trong các phép đo khoa học.
- Kỹ thuật và Công nghiệp: Trong kỹ thuật và công nghiệp, giá trị tuyệt đối được sử dụng để đảm bảo rằng các đại lượng không âm, như áp suất, điện áp, hoặc dòng điện, không vượt quá giới hạn an toàn.
- Xử lý Tín hiệu và Âm thanh: Trong xử lý tín hiệu và âm thanh, giá trị tuyệt đối được sử dụng để biến đổi tín hiệu và loại bỏ âm thanh phản xạ hoặc các yếu tố gây nhiễu.
- Thống kê: Trong thống kê, giá trị tuyệt đối có thể được sử dụng để tính toán các giá trị trung bình và độ lệch chuẩn, đảm bảo rằng các giá trị không âm được sử dụng.
- Lập trình máy tính: Trong lập trình, giá trị tuyệt đối là một phần quan trọng của các hàm toán học và các phép tính, đặc biệt trong việc xử lý dữ liệu và kiểm tra điều kiện.
- Đo lường Thời gian: Trong thực tế, giá trị tuyệt đối thường được sử dụng khi đo lường khoảng thời gian, đảm bảo rằng kết quả là một giá trị không âm.
- Điều khiển và Kiểm soát: Trong lĩnh vực điều khiển và kiểm soát tự động, giá trị tuyệt đối được sử dụng để đảm bảo rằng các tín hiệu điều khiển không bao giờ trở thành âm hoặc âm tích.
- Kiểm soát Tốc độ và Góc độ: Trong việc lái xe hoặc điều khiển các thiết bị cơ khí, giá trị tuyệt đối của tốc độ và góc độ thường được sử dụng để đảm bảo an toàn và chính xác.
- Điện tử và Điện lạnh: Trong lĩnh vực điện tử và điện lạnh, giá trị tuyệt đối thường được sử dụng để đo điện áp, dòng điện, hoặc sự biến đổi trong các thông số kỹ thuật.
Như vậy, giá trị tuyệt đối là một khái niệm quan trọng và có ứng dụng rộng rãi trong nhiều khía cạnh của cuộc sống và khoa học.
Sau khi đọc xong bài viết của chúng tôi các bạn có thể hiểu được giá trị tuyệt đối là gì, tính chất của giá trị tuyệt đối và các dạng bài tập giá trị tuyệt đối.